在双因素方差分析中，受试者被分配到两因子的交叉类别组中，以ToothGrowth数据集为例，随机分配 60  只豚鼠，分别采用两种喂食方法（橙汁或维生素C），各喂食方法中抗坏血酸含量有三种水平（0.5mg,1mg或2mg）,每种处理组合都被分配只豚鼠。牙齿长度为因变量，如下

> attach(ToothGrowth)> table(supp,dose)     #各设计单元中样本大小都相同，表明该设计是均衡设计    dosesupp 0.5  1  2  OJ  10 10 10  VC  10 10 10> aggregate(len, by=list(supp,dose), FUN=mean)  #计算各单元的均值  Group.1 Group.2     x1      OJ     0.5 13.232      VC     0.5  7.983      OJ     1.0 22.704      VC     1.0 16.775      OJ     2.0 26.066      VC     2.0 26.14> aggregate(len, by=list(supp,dose), FUN=sd) #计算各单元的方差  Group.1 Group.2        x1      OJ     0.5 4.4597092      VC     0.5 2.7466343      OJ     1.0 3.9109534      VC     1.0 2.5153095      OJ     2.0 2.6550586      VC     2.0 4.797731> dose <- factor(dose)              #将 does转化问因子，这样aov()函数就将它当作一个分组变量，而不是数值型协变量> fit <- aov(len ~ supp*dose)> summary(fit)            Df Sum Sq Mean Sq F value   Pr(>F)    supp         1  205.4   205.4  15.572 0.000231 ***dose         2 2426.4  1213.2  92.000  < 2e-16 ***supp:dose    2  108.3    54.2   4.107 0.021860 *   #主效应(supp、dose)和交互效应都非常显著Residuals   54  712.1    13.2                     ---Signif. codes:  0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1

• 模型假设检验和均值比较与单因素方差分析一样
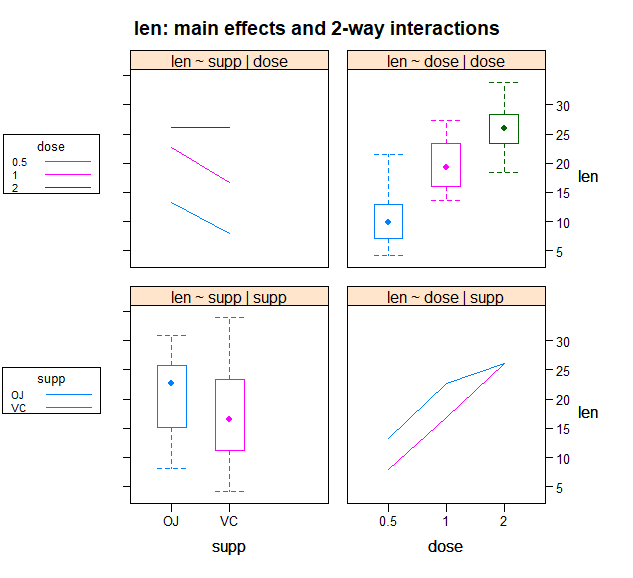
• 数据可视化

> library(HH)> interaction2wt(len~supp*dose) #图形对任意顺序的因子设计的主效应和交互效应都会进行展示，也能展示任意复杂度设计(双因素方差分析、三因素方差分析等)